Om een reeks cijfers samen te vatten wordt vaak een gemiddelde gebruikt. In een vijver die gemiddeld 5 centimeter diep is, kunnen er echter plaatsen zijn die 2 meter diep zijn. Hoe kun je weten of het gemiddelde een reeks cijfers goed omschrijft?
Wat is het nut van statistiek? (deel 1)
Waarom gebruiken onderzoekers zoveel statistiek, wat het onderzoek voor leken soms hopeloos moeilijk maakt?
Een woordje uitleg …
Een belangrijke reden om statistiek te gebruiken, is om het onderzoek duidelijker te maken... Al zullen velen twijfelen aan deze bewering!
Een voorbeeld
Twintig personen krijgen gedurende twee weken een middel om te vermageren (‘interventiegroep’), en deze resultaten worden vergeleken met een placebomiddel bij twintig andere personen (‘controlegroep’). Deze mensen worden gewogen voor en na het onderzoek. Figuur 1 geeft de resultaten weer, namelijk het gewichtsverlies na het onderzoek.
Conclusie: het is niet gemakkelijk om een conclusie te trekken. Werkt het vermageringsmiddel of niet?
Figuur 1. Gewichtsverlies in de interventiegroep en de controlegroep
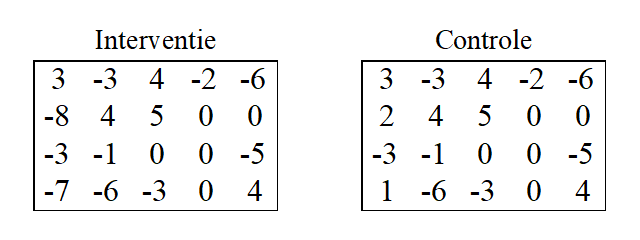
Statistiek zal ons helpen om reeksen getallen op eenvoudige wijze weer te geven. In dit geval kunnen we bijv. het gemiddelde gebruiken (zie figuur 2).
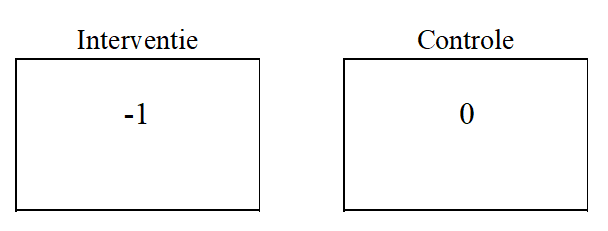
In de interventiegroep, de personen die het vermageringsmiddel kregen, is het gewichtsverlies -1 kg. In de controlegroep, de personen die een placebomiddel kregen, 0 kg. Dat is al een stuk duidelijker.
Door het resultaat op deze manier duidelijk te maken, verliezen we echter informatie. In de interventiegroep bijv. is het gemiddeld gewichtsverlies 1 kg, maar er zijn deelnemers die tot 8 kg verliezen. In de controlegroep zijn er deelnemers die tot 6 kg verliezen. Deze cijfers komen niet tot uiting in het gemiddelde.
Figuur 2. Gewichtsverlies in de interventiegroep en de controlegroep
Standaardafwijking
Er wordt daarom een tweede bewerking gebruikt, die de kwaliteit van het gemiddelde weergeeft. Uit het voorbeeld is -1 kg een goed gemiddelde als alle deelnemers 1 kg verloren, maar dit is niet het geval. Merk op dat -1 kg ook het gemiddelde is van bijv. -20 kg en +18 kg: in dit geval geeft het gemiddelde -1 kg geen goed beeld van de werkelijkheid.
Statistici zeggen in dit geval dat het model (= het gemiddelde) geen goede weergave is van de werkelijkheid.
Om een idee te geven van de kwaliteit van het gemiddelde, gebruikt men de standaarddeviatie of -afwijking: hoe kleiner de standaardafwijking, hoe beter het model een gemiddelde plakt op de werkelijkheid.
Figuur 3. Gewichtsverlies in de interventiegroep en de controlegroep
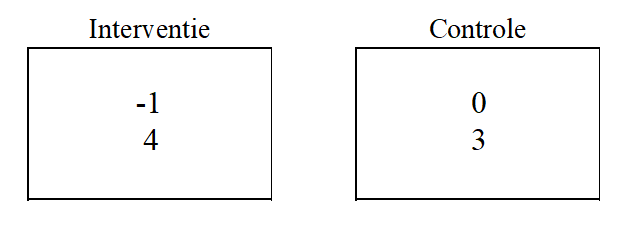
Statistici schrijven dan dat het gemiddelde in de interventiegroep -1 kg (4) was, en in de controlegroep 0 kg (3). Het cijfer tussen haakjes geeft de standaardafwijking weer. Dit cijfer ligt lager voor de controlegroep: dit betekent dat de deelnemers in de controlegroep een meer vergelijkbaar resultaat hadden, terwijl de resultaten in de interventiegroep meer varieerden.

